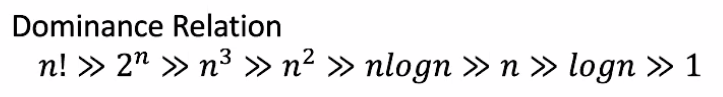COMP10002 Foundations of Algorithms Notes

Nov 1, 2021

SIMILARITIES AND DIFFERENCES FROM PYTHON

Similarities

imperative languages
range of arithmetic and logical operations
range of control structures
- eg. selection, iteration, recursion
function arguments are received as initial values of local variables
libraries are available for a wide range of other operations

Differences

C	Python
program structure indicated by semicolons and braces	program structure by layout
integer arithmetic is bounded; silently overflows
no bool type; uses int	has bool type
static typing; requires declarations	dynamic typing
compiled	interpreted
explicit pointer variables and pointer operations	in-built list, set and dictionary structures and operations

⚠️ GENERAL WARNINGS WHEN OPERATING THE CHAINSAW ⚠️

don't always follow warnings blindly
- Eg. if (x=1) will give a warning and ask you to make it if ((x=1)) but it should be if (x==1)

PROGRAM STRUCTURE

/*
// (1) short description of program, author and date
# Description: Adds pi to a number
# Author: Cindy Chuah
# Date: 05/08/2021
*/

// (2) header file declarations:
#include <stdio.h>

// (3) global declarations
#define PI 3.1415

int main() {
  // (4) local variable declaration:
  int num;

  // (5) statements
  printf("Enter a number: ");
  scanf("%d", &num);

  printf("%d + pi = %.2f", num, num+PI);
}

COMPILING AND EXECUTING

Compiling Command: gcc -Wall -ansi -o [filename] [filename.c]
Running Command: ./[filename]

COMMENTING

/*comment*/ multi-line comments
//comment single-line comment

PRINTING & INPUTTING

printf("format string", var1, var2) displays data (formats defined by the format string) as a string to the output stream
- if successful, total number of characters written is returned
- on failure, a negative number is returned
- eg: printf("I love %s%d", "COMP", 10002)
scanf("format string", &var1, &var2) receives input from keyboard
- &var address of a variable

Format String

contains text to be written to stdout

Placeholder

contain format tags to be replaced by the values specified in subsequent additional arguments and formatted as requested - aka placeholders
Format tags: %[flags][width][.precision][length]specifier
Specifiers
- %c character
- %d or %i signed (can be positive or negative) decimal integer
- %f float
- %lf long float
- %s string of characters
- %p pointer

Control Characters

\n new line
\r carriage return
\" quotation mark
\' apostrophe
\\ backslash

ASSIGNMENT/DECLARATION

#define [CONSTANT] [value] define a constant with value
- type is automatically defined
variable = expression assigns the expression to the variable

DATA TYPES

int integer

⚠️ Integer overflow and underflow

$2^{31}-1=2,147,483,647$

#include <stdio.h>

int
main(int argc, char *argv[]) {
  int big, bp1, bt2, bp1t2;
  big   = 2147483647;
  bp1   = big+1;  // -2147483648 👈
  bt2   = big*2;  // -2 👈
  bp1t2 = bp1*2;  // 0 👈

  /* 👈 = clearly not the correct answers due to iteger overflow
  yet, no warning it given by compiler */

  printf("big=%d, bp1=%d, bt2=%d, bp1t2=%d\n",
    big, bp1, bt2, bp1t2);
  return 0;
}

Fun fact: If Boeing 787 switched on for 248 days, the power shuts off and you fall out of the sky
⚠️ Integer division VS Double division
- 1/2 = 1 (floor/integer division)
- 1.0/2 = 0.5, 1/2.0 = 0.5, 1.0/2.0=0.5
- you must 'infect' the calculation with a double for the result to be a double

str string
- Eg. "string"
char character
- Eg. 'A'
long long integer
float float number

double long float

⚠️ floating point arithmetic and rounding error

use doubles: doubles store approximate values over a much larger range than int variables

int main() {
  double d1, d2, d3;
  d1 = 0.1;
  d2 = d1 + d1 + d1 + d1 + d1 + d1 + d1 + d1 + d1 + d1;
  d3 = d2 - 1.0;
  printf("\n Doubles:\nd1 = %23.20lf\nd2 = %23.20lf\nd3 = %23.20lf\n", d1, d2, d3);


  float f1, f2, f3;
  f1 = 0.1;
  f2 = f1 + f1 + f1 + f1 + f1 + f1 + f1 + f1 + f1 + f1;
  f3 = f2 - 1.0;
  printf("\nFloats:\nf1 = %23.20f\nf2 = %23.20f\nf3 = %23.20f\n", f1, f2, f3);
}

RESULT:
Doubles:
d1 =  0.10000000000000000555
d2 =  0.99999999999999988898
d3 = -0.00000000000000011102

Floats:
f1 =  0.10000000149011611938
f2 =  1.00000011920928955078
f3 =  0.00000011920928955078

THEREFORE, USE ALWAYS USE DOUBLES!!

⚠️ C does not have boolean type
- zero (0) is interpreted as false
- non-zero (1, -23, 87.9 ...) is interpreted as true
- defining true and false:
```
// using #define
#define true 1
#define false 0

// using const
const int true = 1;
const int false = 0
```

[object Object] vs [object Object]

char + int is valid
char holds 4 bytes
int holds 1 byte

OPERATORS (Highest to Lowest Precendence)

note: not every operator is here

Precedence: Postfix -> Unary -> Multiplicative -> Additive -> Coparison/Relational -> Equality -> Logical AND -> Logical OR -> Assignment
⚠️ use parenthesis () so you don't need to remember precedence
Including redundant parentheses costs nothing. Omitting necessary parentheses can cost

Postfix
- a++ post-increment; same as a+=1
- a-- post-decrement; same as a-=1
Unary
- ! logical NOT
  - !(!x) == x BUT, because C uses integers instead of booleans:
    - when x=5:
    - !(!x) => !(!5) => !(0) => 1, which is not x ;-;
- - negative
- + positive
- (type) cast operator
  - converts objects to another type
Multiplicative
- *, /,
- % modulus
  - ⚠️ Cannot include doubles
    - 19.0 % 4.0 and 19.0/4 is illegal
    - 19/4 is legal (result is equal to 3)
Additive
- +, -
Comparison/Relational
- <, >, <=, >=
Equality
- ==, !=
Logical AND
- &&
Logical OR
- ||
Assignment
- =, +=, -=, *=, ...

⚠️ && and || go from left to right
- if (LHS && RHS) {...}
  - if the LHS is false, RHS not evaluated
```
if (y && x/y) {...}
// if y is 0, then x/y will not be evaluated
// and you won't get a 'division by 0' error
```
- if (LHS || RHS) {...}
  - if the LHS is true, RHS not evaluated
other logical expressions: NOT NECCESARILY left to right

CONDITIONALS

[object Object]

if ([guard condition1]) {
    // code to run if condition1 is true
} else if ([guard condition2]) {
    // code to run if condition2 is true
} else {
    // code to run if none of the above conditions are true
}

Example 1: num_neg += (n<0)
- same as
```
if (n<0)
    num_neg += 1;
```

Example 2 (function exit):

/*checks if 3 (integer) inputs are received*/
if scanf("%d%d%d", &n, &m, &r){  // scanf returns number of successfully valid inputs
    printf("scanf failed to read three items\n");
    exit(EXIT_FAILURE);
}

exit(EXIT_FAILURE) terminates program and signals an error
exit(EXIT_SUCCESS) terminates program without signaling an error

eqalinif.c
- make sure you use == to check for equality
- not =, which is used for assignment
danglingelse.c
- use explicit braces when nesting conditions
- compiler doesn't care about indentation
threetest.c
- (4 < 3 < 2)
  - will become ((4 < 3) < 2)
  - since 4 < 3 evaluates to 'true'
    - the compiler will change the value of that to 1
      - (because no booleans in C)
  - the statement will become: (1 < 2)
  - which will evaluate to 'false' (aka 0)!

[object Object]

☠️ Don't use in assignments and exam

never use switch lol
can have different interpretations

switch (variable){
    case ...1:
        // code that runs if the variable is equal to ...1
        break;
    case ...2:
    case ...3:
        // code that runs if the variable is equal to ...2 or ...3
        break;
    default:
        // 'else' code
        break;
}

LOOPS

break ends loop immediately
continue moves on to next iteration

[object Object] loops

for (initialize; guard; update) {
  // statements
}

[object Object] loops

while (guard) {
  // statements
}

// same as
for ( ;guard; ) {  // no initialise and update
  // statements
}

[object Object] loop

☠️ Don't use in assignments and exam

do {
  // statements
}
while (guard)

[object Object] and [object Object]

getchar() returns the character read
- EOF means 'End of File' ('Enter' button)
putchar() prints the character returns the character written

FUNCTIONS

provide a mechanism of abstraction
- simplify to steps
- code organisation
- easy to check that function-step is correct
operations with multiple lines -> create a function
each function should have a single function
choose meaningful function names
variables get deleted after function call finishes
Limitation of functions: can only return 1 value with 1 type


// function signature/prototype
returnType functionName(type1 arg1, type2 arg2, ...);

// function call
functionName(arg1, arg2, ...);

// function definition
returnType functionName(type1 arg1, type2 arg2, ...) {
  // statements
  // return statement
  return [expression];
}

Example (Adding numbers):

#include <stdio.h>
int addNumbers(int a, int b);         // function prototype

int main()
{
    int n1,n2,sum;

    printf("Enters two numbers: ");
    scanf("%d %d",&n1,&n2);

    sum = addNumbers(n1, n2);        // function call
    printf("sum = %d",sum);

    return 0;
}

int addNumbers(int a, int b)         // function definition
{
    int result;
    result = a+b;
    return result;                  // return statement
}

RECURSION

2 main parts
- base case: normally when the function calls should end
- recursive step: usually breaking down the problem into a smaller problem and an iterative step

/*Calculate the nth triangle number using recursion*/
int t_rec(int n) {
  if (n==0) {  // Base Case
    return 0;
  } else {
    return n + t_rec(n-1);  // Recursive Case (make sure to change n)
  }
}

statements before recursive call vs statements after recursive call
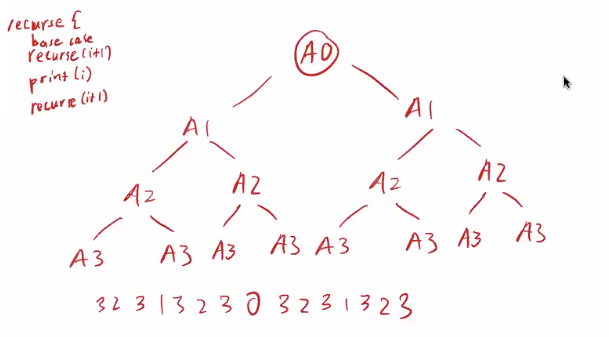
recursion tree

Towers of Hanoi

larger disks cannot be put on top of smaller disks
optimal way to move disks from A to C

[object Object] LIBRARY

Some functions
- sin(x)
- log(x)
- fabs(x) floating point value of x
constants
- M_PI pi
- M_SQRT2 square root of 2

POINTERS

address	value	variable
1052	1048	pointer
1048	5	var

special type of variable
int *px pointer variable declaration
- type of pointer can also be void
px = &x store address of x in pointer variable
*px returns value in address
- printf("%d", *px) // prints value of x
px returns the address stored in px (aka address of x, &x)
Stack Oveflow
- an undesirable condition in which a particular computer program tries to use more memory space than the call stack has available

SCOPE

scope heirarchy
- local variable -> local static variable/function arg variable -> global variable
global scope
- ❗ refrain from using global variables
- stored in data
- can be used in any function in the program
static [type] [var] modifier - only runs initialisation once - variable in function holds value
- stored in data segment
- allow functions to maintain state from one call to the next without being accible to other functions
- Use case: counting number of times function was called
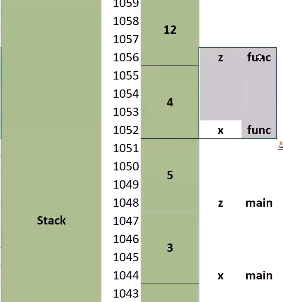
local scope
- stored in stack
- declared inside functions
- can only be used within the function
- even if variable names are the same, a variable in a function does not affect and is not the same as a varibale in another function

int global;   // stored in data
int func(int argvar);
int main() {
  int mainlocal;  // stored in stack (main is also a function)
  ...
}
int func(int argvar) {
  int funclocal;  // stored in stack
  ...
  // funclocal -> static/argvar -> global
}

ARRAYS

❗ There is no execution-time array bounds checking, and responsibility rests with the programmer
- "I must not use a value of i that is outside the range of the array"
size of each element in array must be declared
don't need to declare number of elements

#define N 5  // hash define for array size

int main (int argc, char *argv[]) {
  int A[N];  // array declaration

  // fill in array
  for (int i = 0; i<N; i++) {
    A[i] = i*(i+1)/2;
  }

  printf("array has been filled\n");

  // print array
  for (i=0; i<N; i++){
    printf("A[%d]=%d\n", i, A[i]);
  }

  return 0;

}

A[n] an array of n variables
A pointer constant
- stores address of first variable in the array &A[0]
we can also use pointers to access arrays
- we can add/subtract pointers
int Y[5][10] 2D array declaration
- Y is an arary of 5 arrays of 10 ints
- when 2D arrays are passed to functions, only the dominant dimension can be left unspcified func(A[][COLS])
arrays can be initialized on declaration by supplying a list of values in braces
- int arr[2] = {1, 2}
always #define array sizes to avoid magic numbers

INSERTION SORT

void int_swap(int *num1, int *num2) {
    int temp = *num1;
    *num1 = *num2;
    *num2 = temp;
}

void insertion_sort(int A[], int n) {
    for (int i=1; i<n; i++) {
        for (int j=i-1; j>=0; j--) {
            if (A[j+1]<A[j]) {
                int_swap(&A[j], &A[j+1]);
            }
        }
    }
}

best case: $O(n)$
- array already sorted
worst case: $O(n^2)$
average case: $O(n^2)$

SELECTION Sort

void int_swap(int *num1, int *num2) {
    int temp = *num1;
    *num1 = *num2;
    *num2 = temp;
}

void selection_sort(int A[], int n) {
    for (int i=n-1; i>0; i--){
        // scan through array
        int largest = 0;
        int largest_index = 0;
        int j;

        for (j=0; j<=i; j++){
            // found largest
            if (A[j] > largest){
                largest = A[j];
                largest_index = j;
            }
        }
        int_swap(&A[largest_index], &A[i]);
    }
}

best case: $O(n^2)$
- array already sorted
worst case: $O(n^2)$
- array is soretd BUT the smallest element is the last element (eg. 2, 3, 4, 5, 6, 1)
average case: $O(n^2)$

QUICKSORT

divide and conquer algorithm
- using extreme elements as pivot element: $O(n^2)$
best case: $O(n\log n)$
- partition process always picks the middle element as pivot
worst case: $O(n^2)$
- partition process always picks extreme elements (smallest or largest) elements as pivot
average case: $O(n\log n)$

Proving Correctness

...

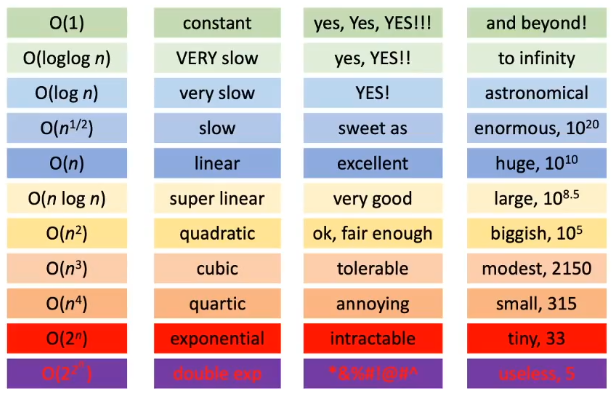
BIG O

ALGORITHMS

heart of computing

Correctness

assertions: argued statements about what must be true as a program executes
with the use of logic, and precise rules associated with the semantics of executable statements, invariants can be used to provide formal proofs of program correctness
Example: Linear Search
P is loop invariant
assert(...) pseudo-function to do your own array bounds checking

Efficiency

memory space required
execution time

Example: Linear Search
- best case: item x found in first location
- worst case: item notfound
  - n loop iterations required

LINEAR SEARCH

unsorted
sorted
- still O(n)

BINARY SEARCH

only for sorted array
Invariant
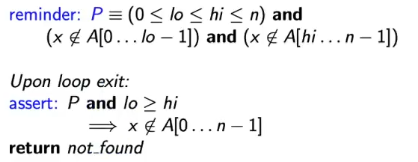
- important to demonstrate that loops terminate

/* recursive binary search
*/
int binary_search(data_t A[], int lo, int hi, data_t *key, int *locn){
  int mid, outcome;
  if (lo >= hi) {
    return BS_NOT_FONUD;
  }
  mid = (lo+hi)/2;
  if ((outcome = cmp(key, A+mid)) < 0) {
    return binary_search(A, lo, mid, key, locn);
  } else if (outcome > 0) {
    return binary_search(A, mid+1, hi, key, locn);
  } else {
    *locn = mid;
    return BS_FOUND;
  }
}

cmp(A, B) comparison function
- usually passed into sorting/searching functions as a function argument
- compares two elements A and B
- returns:
  - -ve if A comes before B
  - 0 if A and B are equal
  - +ve if A come after B
Time Complexity: O(log n)

[object Object]

another layer of abstraction

#define SIZE 5

typedef double vector_t[SIZE]
typedef vector_t sqmatrix_t[SIZE]

int main() {
  vector_t A, B;
  // A and B are vectors of 5 doubles
  sqmatrix_t C;
  // C is a vector of 5 vectors of 5 doubles
}

STRINGS

array of type char // character pointer
include <string.h>
'\0' null byte - signifies end of string
- char str1[10] = {'h', 'i', '\0'}
- char str1[11] = "helloworld" or char *p = "Hello World
  - adds nullbyte implicitly
  - array must have enough space for nullbyte
printf/scanf using %s
- printf("%s", str1)`
- scanf("%s", str2)
  - don't need & because the string is a pointer
  - implicitly adds null-byte at the end
strlen(char *str1) returns length of string
strcpy(char *dest, char *src) copies string from src_str to dex_str
strncpy(char *dest, char *src, int n) copies n characters from src to dest
- dest must be at least n bytes long
strcmp(char *str1, char *str2) for comparing strings
- we cannot use == because comparing pointers (address)
strncmp(char *str1, char *str2) compares n characters in str1 and str2
strcat(char *dest, char *src) appends a copy of src to dest by overwriting its null byte
- dest must be large enough to acoommodate the extended string
- Risky
strncat(char *dest, char *src, int n) copies n characters from src to the end of dest, replacing its null-byte
atoi(char *s) returns the integer value represented by the characters of s
atof(char *s) returns the double value represented by the character of s
isalpha() returns 1 if character is an alphabetical character and 0 otherwise

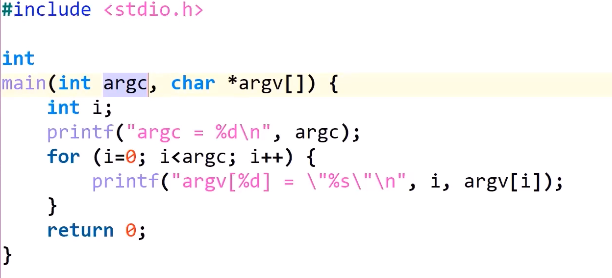
[object Object]

allows us to store comand line arguments
char* argv[]
- array of pointers (that point to strings)
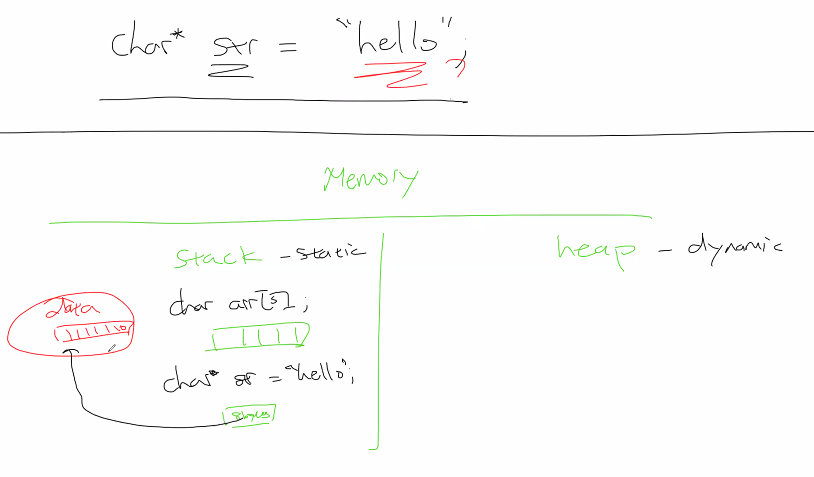
- cannot access when declared in data
why useful
- reading files
- more input ways

PATTERN-MATCHING ALGORITHMS

Given: A text sequence T[0 ... n-1] and a pattern P[0 ... m-1]
Question: Does pattern P appear as a continuous subsequence of text T? If so, where?

Sequential pattern search

void naive_search(char* T, char* P) {
    int n = strlen(T);
    int m = strlen(P);
    int found = FALSE;

    int s=0;
    while (s <= n-m) {
        int i;

        for (i=0; i<m; i++){
            if (T[s+i] != P[i]){
                break;
            }
        }

        if (i == m){
            printf("Found at %d\n", s);
            found = TRUE;
        }

        s++;
    }

    if (!found) {
        printf("Not Found\n");
    }
}

Best Case: O(n)
- first character in pattern is not in text
- Text: aaaaaaaaaaaaaaaa
- Pattern: baa
Worst Case: O(nm)
- last character in pattern is not in text
- Text: aaaaaaaaaaaaaaaa
- Pattern: aaab
Average Case: O(n)

Knuth-Morris-Pratt (KMP) Search

❗ in exam
- understand how it works - don't memorise the code
Problem: Find substring in text
- does "aab" occur in "aaacabaabaa"
Brute Force
- compare substring at every index in the text
- time complexity: $O(mn)$
  - m = length of substring
  - n = length of text
Knuth-Morris-Pratt KMP search
- if mismatch occurs, shift the pattern forward as far as possible without moving past any matching prefix of the pattern
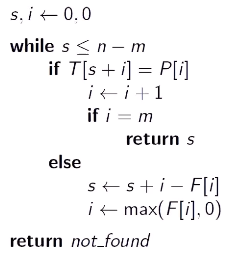
Failure Array
- Define F[i] to be the maximum k<i such that P[0 ... k-1] matches P[i-k ... i-1], with F[0] set to be -1
- At each mismatch, can shift P right by i (mismatch position) minus F[i] (allowance for pattern self-overlap)
- If F[i] is zero, then pattern search resumes from mismatched location s+i, rather than s+1
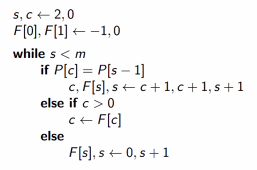
- how to find failure array:
  - first 2 elements: [-1, 0]
  - "How many suffix is also a prefix?"
  - other elements are 0
- Average less than O(2m)
Average case O(m + n)
- generally, O(m+n) < O(2m)
- because m <= n

Boyer-Moore Horspool (BMH) Search

https://www.geeksforgeeks.org/boyer-moore-algorithm-for-pattern-searching/
best case: O(n / m)
worst case:
average case: O(n)

Suffix Array

generate n suffix strings of text
sort these suffix string
- using ternary quicksort
build time: O(n^2 log(n))
search in suffix array: O(m log(n))
- m << n
why declare a suffix array (when the build time is bigger)?
- amortize complexity
  - which operation is used the most?
    - searching
- building is only done once * can be pre-computed

KMP Search VS BMH Search

KMP
- skip comparisons based on comparisons that we have alread done
  - suffixes that are prefixes
BMH
- comparing starting at the end of the substring
- assuming that if we don't get a match at the end, we don't need to compare at the start

Structs

struct names end with _t

// struct for storing date of births
typedef struct {
  int day;
  int month;
  int year;
} dob_t;

// create a profile struct for storing student profiles
struct profile {
  char name[20];
  int age;
  int student_id;
  dob_t dob;
}
typedef struct profile profile_t;

int main(int argc, char* argv[]){

  // create an instance of the struct
  profile_t student;

  // setting int values
  student.age = 21;
  student.student_id = 321456;

  // setting string values
  strcpy(student.name, "Jane")
}

has component name
student.age = 21
strcpy(var.student, "Jane")
Arrays VS Structures
- structures: can store different types
- arrays: storing different instances of the same type
- arrays: assuming that every element is independent of each other
- eg. date - should be struct, even though they are all int

structures get copied

profile_t temp = var;  // var is a copy of profile_t
temp.age = 100;  // only temp's age

student->age = 32 dereferencing and accessing - to change value of variable using functions
- same as (*student).age = 32

Dynamic Memory

size_t sizeof(thing) returns the number of bytes required to store the type or variable thing
- not really a function
malloc() dynamically declares arrays
- int* array = (int*)malloc(sizeof(int) * 10) dynamically declares 10 ints into an array
- using malloc in function - array doesn't get destroyed (even though it's local):
```
int* give array() {
  int* array = (int*)malloc(sizeof(int) * 10);
  assert(array)
  return array;
}
```
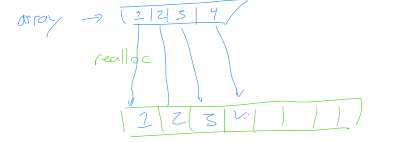
realloc()
- array = (int*)realloc(array, sizeof(int) * 20) changes size of array
- O(n) time complexity

// read in num_rows
big_arr =  malloc(sizeof(int) * num_rows)
for (int i=0; i<num_rows; i++){

}

QUIZ 2

string functions
type compatibility
- ✅ pointer + string/character
- ❌ pointer + pointer

Structs VS Arrays

Assigned (=)
- Array: No
  - B=A does not copy the array
Compared (==)
Argument to function
Returned to function
Take address of (&)
Use as pointer (*, [])
double has alignment requirement
- has to start on multiple of 8

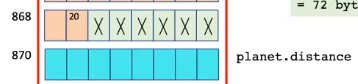
Linked Lists

node1 (head)        node2               node3 (foot)
+------+------+     +------+------+     +------+------+
| data | next | --> | data | next | --> | data | next |
+------+------+     +------+------+     +------+------+

#include <assert.h>

typedef struct node node_t

struct node {
  int data;
  node_t* next;
}

node_t* make_new_node(int data);

int main(int argc, char* argv[]) {
  // Declare a local linked list
  node_t* head = NULL;
  node_t* tail = NULL;

  int input;
  while(scanf("%d), &input) == 1) {
    // Want to make a node
  }
}

node_t* make_new_node(int data) {
  node_t* newnode = (node_t*)malloc(sizeof(node_t))
  assert(newnode)

  newnode->data = data;
  newnode->next = NULL;

  return newnode;
}

Make a new node

Appending to head

malloc a new node
make new node point to head
change the head to be the new node

Appending to tail

malloc a new node
make tail point to new node
change the tail to be the new node

Append in between

make temp traverse through linked list
newnode->next = temp->next

Binary Search Trees

Worst case: Stick

int is_stick(node_t* root){
  if (root->left && root->right) {
    return FALSE;
  }
  if (!root->left || !root->right)
  return is_stick(root->left) && is_stick(root_right);
}

use recursion

In-order traversal

void traverse(root) {
  if (root) {
    traverse(root->left);
    printf(root->data);
    traverse(root->right);
  }
}

Pre-order traversal

used for copying trees

void traverse(root) {
  if (root) {
    printf(root->data);
    traverse(root->left);
    traverse(root->right);
  }
}

Post-order traversal

used for deleting/freeing trees

void traverse(root) {
  if (root) {
    traverse(root->left);
    traverse(root->right);
    printf(root->data);
  }
}

Arrays, LInked Lists and BST Summary

Operation	Array(unsorted)	Linked List(unsorted)	Array(sorted)	BST(balanced)
Search	$O(n)$	$O(n)$	$O(\log n)$	$O(\log n)$
Insert	$O(1)$	$O(1)$(to head)<br>$O(n)$(to tail)	$O(n)$	$O(\log n)$
Remove	$O(n)$	$O(n)$	$O(n)$	$O(\log n)$

Number Representations

Two's Complement Integers

File Operations

in <stdio.h>
3 files that are always provided when a program is executing:
- stdin input from keyboard; can be redirected using <
  - printf(...) is a call to fprintf(stdout, ...)
- stdout output to screen; can be redirected using >
  - scanf(...) is a call to fscanf(stdin, ...)
- stderr error output
  - generated using fprintf(stderr, "xx", yy)
FILE* filepointer declaring filepointers
fopen(const char *filename, const char *mode) returns file pointer to the opened file
- filename string containing name of file to be opened (please #define this)
- mode access mode string:
  - "r" open for reading
  - "w" creates empty file for writing. If file already exists, previous contants deleted at moment of opening
  - "a" open for appending, previous contents retained
  - "r+" open for reading and writing
  - "w+" creates empty file for reading and writing
  - "a+" opens file for reading and appending
freopen(const char*filename, const char *mode, FILE *stream) return pointer to an object identifying the stream, if file oe-opened successfully - otherwise, null pointer is returned
- filename and mode same as fopen(...)
- stream pointer to FILE object that identifies stream to be re-opened
fread(void *ptr, size_t size, size_t nmenb, FILE *stream) returns total number of elements successfully read
- ptr pointer to the array of elements to be read
- size size in bytes of each element to be read
- nmemb number of elements, each one with a size of size bytes
- stream pointer to a FILE object that specifies an input stream
fwrite(void *ptr, size_t size, size_t nmemb, FILE *stream) returns total number of elements successfull written
- ptr pointer to the array of elements to be written
- size size in bytes of each element to be written
- nmemb number of elements, each one with a size of size bytes
- stream pointer to a FILE object that specifies an output stream
fclose() close a file

/* Writing to a text file */
#include <stdio.h>
#include <stdlib.h>

int main()
{
   int num;
   FILE *fptr;

   // use appropriate location if you are using MacOS or Linux
   fptr = fopen("C:\\program.txt","w");

   if(fptr == NULL)
   {
      printf("Error!");
      exit(1);
   }

   printf("Enter num: ");
   scanf("%d",&num);

   fprintf(fptr,"%d",num);
   fclose(fptr);

   return 0;
}

/* Reading from a text file */
#include <stdio.h>
#include <stdlib.h>

int main()
{
   int num;
   FILE *fptr;

   if ((fptr = fopen("C:\\program.txt","r")) == NULL){
       printf("Error! opening file");

       // Program exits if the file pointer returns NULL.
       exit(1);
   }

   fscanf(fptr,"%d", &num);

   printf("Value of n=%d", num);
   fclose(fptr);

   return 0;
}

Floating Point Numbers (IEEE754)

Algorithm
1. Convert the decimal into binary
  - eg. 14.25 -> 1110.01
    - 14 = 8 + 4 + 2 + 0
    - 0.25 = 0*1/2 + 1*1/4
2. Convert the binary number to 1.xxx... * 2^(pow)
  - eg. 1.11001 * 2^3
    - moved decimal point 3 to the left
3. Mantissa: xxx...
  - eg. 11010000...000 (until 23bits)
4. Exponent: pow + const in base 2
  - const: 127 for 32-bit
  - eg. 3 + 127 = 130 -> 10000010
5. Sign bit is either +ve or -ve
  - eg. 32-bit floating point num: 0 10000010 11001000...000
32-bit floating point Numbers
1 bit 8 bits 23 bits
sign exponent mantissa
- bits can be different in exam

1 bit	8 bits	23 bits
sign	exponent	mantissa

Octal

base 8 (2^3)
0, 1, 2, 3, 4, 5, 6, 7

Hexadecimal

base 16 (2^4)
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f

Monte Carlo Methods

Use pseudo-random number generation to allow modeling of a physical system
srand() initialize random-number sequence
rand() returns next seemingly-unrelated int in the sequence

Stack

LIFO: Last in, First out
Operations to be supported
- S <- stack_create_empty()
- stack_is_empty(S)
- S' <- stack_push(S, item)
- item <- stack_top(S)
- S' <- stack_pop(S)
Implementation Options: Array (with realloc), Linked List
All operations should take O(1) time

typedef struct {
  int *arr;
  size_t count, max_size;
} stack_t;

#include <stdlib.h>
#include <assert.h>

#define STACK_SIZE 10

typedef struct {
  int *arr;
  size_t count, max_size;
} stack_t;

stack_t *create_empty_stack(void) {
  stack_t *s = (stack_t *) malloc(sizeof(stack_t));
  s->arr = (int *)malloc(STACK_SIZE*sizeof(int));
  assert(s && s->arr);

  s->count = 0;
  s->max_size = STACK_SIZE;
  return s;
}

void recursive_print(stack_t *stack, size_t depth) {

}

Queue

FIFO: First In First Out
Operations to be supported
- Q <- queue_create_empty()
- queue_is_empty()
- Q' <- queue_append(Q, item)
- item <- queue_head(Q)
- Q' <- queue_tail(Q)
Implementation options: Circular Array, Linked List
All operations should take O(1) time

Priority Queue

Operations to be supported:
- Q <- pq_create_empty()
- pq_is_empty(Q)
- Q' <- pq_insert(Q, item, priority)
- item <- pq_max_priority(Q)
- Q' <- pq_delete_max(Q)
Implementation options:
Operation Cost:

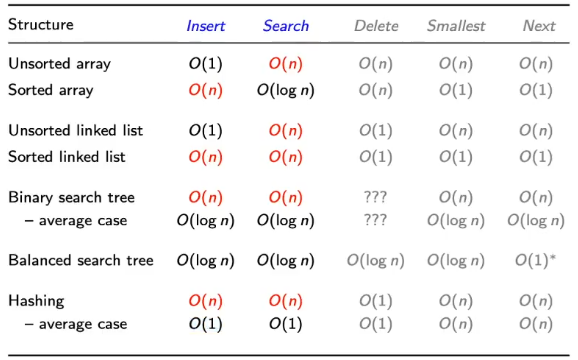
Dictionary

Operations to be supported
- D <- dict_create_empty()
- dict_is_empty(D)
- D' <- dict_insert(D, item, key)
- item <- dict_search(D, key)
- D' <- dict_delete_item(D, key)
plus(maybe):
- item <- dict_smallest(D)
- item' <- dict_next_element(D, item)
Implementation options

Hashing

Hashing Function, h(): deterministically construct a semmingly-random integer
- depends on initial seed so it is reusable
- never just add character values or shift-n-add -- not enough randomness
Collisions: when different values get same hash value
- Birthday Paradox: In a room of 23 people, there is a 50-50 chance of at least 2 people habing the same birthday
Buckets
- use linked lists

Mergesort

mergesort(A[0...n-1])
  if n<=1
    // already sorted
    return
  // [1] split into 2 parts
  mid = n/2
  // [2] recursively sort each part
  mergesort(A[0...mid-1]) // sort first half
  mergesort(A[mid...n-1]) // sort second half
  merge(A[0...mid-1], A[mid...n-1])

Divide-and-conquer
Difference with Quicksort:
- Quicksort: "Hard split, easy join"
- Mergesort: "Easy split, hard join"

split into 2 parts

void
merge_sort(data_t A[], int n) {
  data_t *T;
  T = malloc((n/2)*sizeof(*T));
  assert(T != NULL);
  recursive_merge_sort(A, n, T);
  free(T);
}

recursive call: to sort each part

static void
recursive_merge_sort(data_t A[], int n, data_t T[]) {
  int mid;
  if (n<=1) {
    return;
  }
  mid = n/2;
  recursive_merge_sort(A, mid, T);
  recursive_merge_sort(A+mid, n-mid, T);
  merge(A, mid, n, T);
}

merge

static void
merge(data_t A[], int mid, int n, data_t T[]) {
  /* merge array sections A[0..mid-1] and A[mid..n-1] */
  int i, s1, s2;
  /* copy first section into temporary array T */
  for (i=0; i<mid; i++) {
    copy_data(T+i, A+i);
  }
  i = 0;
  s1 = 0; s2 = mid;
  /* merge second section at A[mid] with T, putting output
    back into section starting at A[0] */
  while (s1<mid && s2<n) {
    if (cmp(T+s1,A+s2) < 0) {
      /* element from T goes next */
      copy_data(A+i, T+s1);
      s1 += 1;
    } else {
      /* element from A goes next */
      copy_data(A+i, A+s2);
      s2 += 1;
    }
    i += 1;
  }
  while (s1<mid) {
    /* copy over any remaining elements in T */
    copy_data(A+i, T+s1);
    s1 += 1;
    i += 1;
  }
  /* all elements are now in their final positions */
}

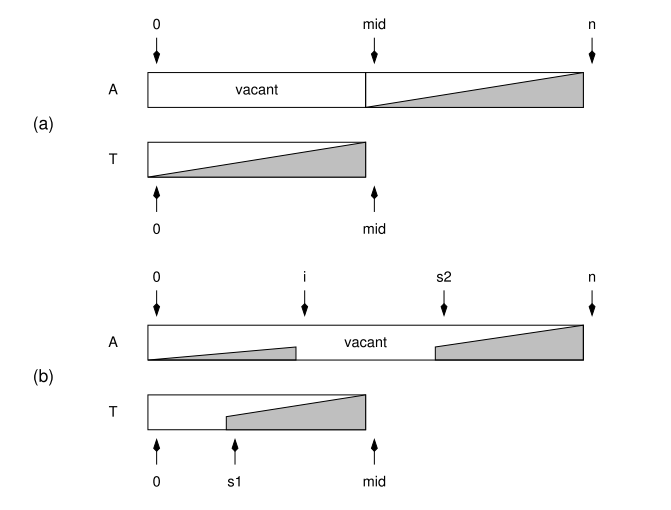
Worst case: $O(nlog n)$
Cons: takes extra space

Heapsort

Create an implicitly balanced tree based on array positions
- array: A[0...n-1]
- for item A[i]
  - children: A[2i+1] and A[2i+2]
  - parent: A[(i-1)/2]
Make it a heap

Rule: no child may be larger than its parent

A[i] <= A[(i-1)/2]

void
sift_down(data_t A[], int parent, int n) {
  int child;
  if ((child = 2*parent+1) < n) {
    /* there is at least one child to be checked */
    if (child+1<n && cmp(A+child, A+child+1)<0) {
      /* the right child exists, and is larger */
      child += 1;
    }
    if (cmp(A+parent, A+child)<0) {
      /* parent is smaller than larger child */
      swap_data(A+parent, A+child);
      sift_down(A, child, n);
    }
  }
}
void
build_heap(data_t A[], int n) {
  int i;
  for (i=n/2-1; i>=0; i--) {
    sift_down(A, i, n);
  }
}

Heapsort

void
heap_sort(data_t A[], int n) {
  int active;
  build_heap(A, n);
  for (active=n-1; active>0; active--) {
    swap_data(A+0, A+active);
    sift_down(A, 0, active);
  }
}

best case: $O(n\log n)$
worst case: $O(n^2)$
average case: $O(n\log n)$
Pro: No extra space required